Gagak Hitam

Arithmetic & Logic Unit

Does the calculations
Everything else in the computer is there to service this unit
Handles integers
May handle floating point (real) numbers

Data types

Represented in binary-coded form
Only have 0 & 1 to represent everything
Can be classified to these categories:

1. Numbers used in arithmetic computation

2. Letters of the alphabet used in data processing

3. Other discrete symbols used for specific purpose

Alphanumeric Representation

An alphanumeric character set is a set of elements that includes the 10 decimal digits, the 26 letters of the alphabet and a number of special character such as $, +, and =.

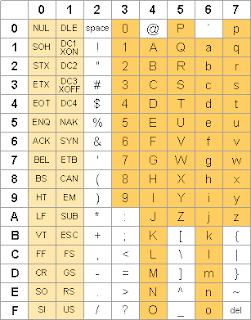
The standard alphanumeric binary code: ASCII (American Standard Code for Information Interchange) uses seven bits to code 128 characters.

Diagram 1: ACSII Code

Alphanumeric Representation

Codes must be in binary because registers can only hold binary information.

Another alphanumeric code used in IBM equipment; EBCDIC (Extended BCD Interchange Code) that uses 8 bits for each character.

BCD (Binary Coded Decimal) represents each individual digit of a decimal number as a group of binary bits; the other formats would convert an entire decimal value to its equivalent binary value. *In the 8421 Binary Coded Decimal (BCD) representation each decimal digit is converted to its 4-bit pure binary equivalent.

Example Decimal to Binary Coded Decimal (BCD)

Number Bases

Different Bases

Decimal --------- (base 10)

Binary ---------- (base 2)

Octal ----------- (base 8)

Hexadecimal ---- (base 16)

The Decimal Number Systems

The decimal system uses 10 as a base, and the 10 digits available are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Depending on its position in the whole number.

For example, the decimal number 9348 represents:

For example, the decimal number 0.258 represents:

For example, the decimal number 7534.448 represents:

The Binary Number Systems

The binary system uses 2 as its base with the digits 0 and 1.

Let’s look at 110100 as an example of a binary number.

Example 1001.101 of a binary number.

In summary, what you need to be able to understand is that the value that is represented by a digit depends on the digit’s position within the number and the base of the numeric system used. With every move of a digit to the right the value represented decrease by a power of the base.

Decimal to Binary Conversion

Integer and fractional parts are handled separately.

Example 19.6875 (base 10) to Binary.

The Octal Number System

Base-8 number system.
In octal numerals each place is a power with base 8.
Uses the digits 0,1,2,3,4,5,6,7.

Example Octal to Decimal: 122 (base 8)

Example Decimal to Octal: 1028 (base 10)

Octal to/from Binary

The binary numbers should be grouped into 3 numbers each as 2 (power 3) = 8.

Example Binary to Octal: 1111101.1001 (base 2)

Example Octal to Binary: 56.3 (base 8)

The Hexadecimal Number System

16 Hexadecimal Digits: 0 – 9, A – F
More convenient to use than binary numbers
Binary digits are grouped into sets of four bits.

Binary, Decimal, and Hexadecimal Equivalents

Example Binary to Hexadecimal: 1110 1011 0001 0110 1010 0111 1001 0100

Hexadecimal to Decimal

Multiply each digit by its corresponding power of 16

Example Hexadecimal to Decimal: 1234 (base 16)

Decimal to Hexadecimal

Repeatedly divide the decimal integer by 16
Each remainder is a hex digit in the translated value

Example:

If you don't understand what I was explain. Watch this video:

Instruction set architecture is the structure of a computer that a machine language programmer or a compiler must understand to write a correct, timing independent program for that machine.

Elements of a machine instruction:

Operation code (opcode)
Source operand reference
Result operand reference
Next instruction reference

Obtain instruction from program storage

Determine required actions and instruction size

Locate and obtain operand data

Compute result value or status

Deposit results in storage for later use

Source and result operands can be in one of four areas:

main or virtual memory
I/O device
processor register
Immediate

A simple instruction format represented by a sequence
of bits

Instruction types:

data processing: arithmetic and logic instructions
data storage: memory instructions
data movement: I/O instructions
program flow control: test and branch instructions

Number of addresses

Types of operand:

Addresses
numbers
characters
logical data

Processor actions for various types of Operations

Addressing Modes and Formats

Immediate Addressing:

Simplest form of addressing
Operand = address field
e.g. ADD 5 - Add 5 to contents of accumulator, 5 is operand

Direct Addressing

Address field contains address of operand
Effective address (EA) = address field (A)
e.g. ADD A - Add contents of cell A to accumulator, Look in memory at address A for operand

Indirect Addressing

Memory cell pointed to by address field contains the address of (pointer to) the operand
EA = (A)
e.g. ADD (A) - Add contents of cell pointed to by contents of A to accumulator

Similar to direct addressing, the only difference is that the address field refers to a register rather than a main memory address
EA = R

Displacement Addressing

Combines the capabilities of direct addressing and register indirect addressing
EA = A + (R)

Relative Addressing

A version of displacement addressing
R = Program counter, PC
EA = A + (PC)

Base-Register Addressing

A holds displacement
R holds pointer to base address
R may be explicit or implicit
e.g. segment registers in 80x86

Indexed Addressing

A = base
R = displacement
EA = A + R

Stack Addressing

Operand is (implicitly) on top of stack
A stack is a reserved block of locations
e.g. ADD - Pop top two items from stack and add

Instruction Formats

> Define the layout of the bits of an instruction, in terms of its constituent fields

> Must include an opcode and, implicitly or explicitly, indicate the addressing mode for each operand

> For most instruction sets more than one instruction format is used

Allocation of Bits:

Number of addressing modes
Number of operands
Register versus memory
Number of register sets
Address range
Address granularity

For this chapter, i'll explain the purpose and function of Memory System Architecture.

Early computers use the likes of vacuum tubes, switching elements, mercury delay lines and etc. They are very expensive and unreliable.

Then, magnetic cores were introduced in the 1960's. The core represents 1-bit of information. It can be magnetized in two ways ( clockwise and anticlockwise ). Still, it was very expensive and slow.