Data Representation

Arithmetic & Logic Unit

• Does the calculations
• Everything else in the computer is there to service this unit
• Handles integers
• May handle floating point (real) numbers

Data types

• Represented in binary-coded form
• Only have 0 & 1 to represent everything
• Can be classified to these categories:

1. Numbers used in arithmetic computation

2. Letters of the alphabet used in data processing

3. Other discrete symbols used for specific purpose

Alphanumeric Representation

An alphanumeric character set is a set of elements that includes the 10 decimal digits, the 26 letters of the alphabet and a number of special character such as $, +, and =.

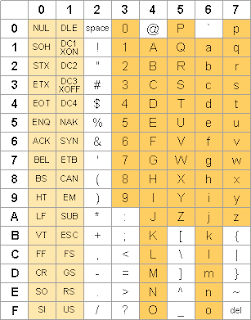
The standard alphanumeric binary code: ASCII (American Standard Code for Information Interchange) uses seven bits to code 128 characters.

Diagram 1: ACSII Code

Alphanumeric Representation

• Codes must be in binary because registers can only hold binary information. 

Another alphanumeric code used in IBM equipment; EBCDIC (Extended BCD Interchange Code) that uses 8 bits for each character.

• BCD (Binary Coded Decimal) represents each individual digit of a decimal number as a group of binary bits; the other formats would convert an entire decimal value to its equivalent binary value. *In the 8421 Binary Coded Decimal (BCD) representation each decimal digit is converted to its 4-bit pure binary equivalent. 

Example Decimal to Binary Coded Decimal (BCD)

Number Bases

Different Bases

Decimal --------- (base 10)

Binary  ---------- (base 2)

Octal  ----------- (base 8)

Hexadecimal ---- (base 16)

The Decimal Number Systems

• The decimal system uses 10 as a base, and the 10 digits available are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
• Depending on its position in the whole number.

For example, the decimal number 9348 represents:

For example, the decimal number 0.258 represents:

For example, the decimal number 7534.448 represents:

The Binary Number Systems

The binary system uses 2 as its base with the digits 0 and 1.

Let’s look at 110100 as an example of a binary number.

Example 1001.101 of a binary number.

In summary, what you need to be able to understand is that the value that is represented by a digit depends on the digit’s position within the number and the base of the numeric system used. With every move of a digit to the right the value represented decrease by a power of the base.




Decimal to Binary Conversion

Integer and fractional parts are handled separately.

Example 19.6875 (base 10) to Binary.

The Octal Number System

• Base-8 number system.
• In octal numerals each place is a power with base 8.
• Uses the digits 0,1,2,3,4,5,6,7.

Example Octal to Decimal: 122 (base 8)

Example Decimal to Octal: 1028 (base 10)

Octal to/from Binary

The binary numbers should be grouped into 3 numbers each as 2 (power 3) = 8.

Example Binary to Octal: 1111101.1001 (base 2)

Example Octal to Binary: 56.3 (base 8)

The Hexadecimal Number System

• 16 Hexadecimal Digits: 0 – 9, A – F
• More convenient to use than binary numbers
• Binary digits are grouped into sets of four bits.

Binary, Decimal, and Hexadecimal Equivalents

Example Binary to Hexadecimal: 1110 1011 0001 0110 1010 0111 1001 0100

Hexadecimal to Decimal

Multiply each digit by its corresponding power of 16

Example Hexadecimal to Decimal: 1234 (base 16)

Decimal to Hexadecimal

• Repeatedly divide the decimal integer by 16
• Each remainder is a hex digit in the translated value

Example:

If you don't understand what I was explain. Watch this video: